Polar space

In mathematics, in the field of combinatorics, a polar space of rank n (n ≥ 3), or projective index n−1, consists of a set P, conventionally the set of points, together with certain subsets of P, called subspaces, that satisfy these axioms :

Every subspace, together with its own subspaces, is isomorphic with a projective geometry PG(d,q) with −1 ≤ d ≤ (n−1) and q a prime power. By definition, for each subspace the corresponding d is its dimension.
The intersection of two subspaces is always a subspace.
For each point p not in a subspace A of dimension of n−1, there is a unique subspace B of dimension n−1 such that A∩B is (n−2)-dimensional. The points in A∩B are exactly the points of A that are in a common subspace of dimension 1 with p.
There are at least two disjoint subspaces of dimension n−1.

A polar space of rank two is a generalized quadrangle.

Examples

In PG(d,q), with d odd and d ≥ 3, the set of all points, with as subspaces the totally isotropic subspaces of a random symplectic polarity, forms a polar space of rank (d+1)/2.
Let Q be a nonsingular quadric in PG(n,q) with character ω. Then the index of Q will be g = (n+w−3)/2. The set of all points on the quadric, together with the subspaces on the quadric, forms a polar space of rank g+1.
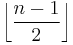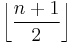Let H be a nonsingular Hermitian variety in PG(n,q²). The index of H will be $\left\lfloor \frac{n-1}{2}\right\rfloor \,\!$ . The points on H, together with the subspaces on it, form a polar space of rank $\left\lfloor\frac{n%2B1}{2}\right\rfloor \,\!$ .

Classification

Jacques Tits proved that a finite polar space of rank at least three, is always isomorphic with one of the three structures given above. This leaves only the problem of classifying generalized quadrangles.